등가응력 사각형의 적용

 등가응력 사각형의 적용

EN 1992-1-1:2004

3.1.7 Stress-strain relations for the design of cross-sections

(3) A rectangular stress distribution (as given in Figure 3.5) may be assumed. The factor λ, defining the effective height of the compression zone and the factor η, defining the effectivestrength, follow from:

λ = 0,8 for fck ≤ 50 MPa  (3.19)

λ = 0,8 - (fck -50)/400 for 50 < fck ≤ 90 MPa (3.20)

and

η = 1,0 for fck ≤ 50 MPa  (3.21)

η = 1,0 - (fck -50)/200 for 50 < fck ≤ 90 MPa (3.22)

Note: If the width of the compression zone decreases in the direction of the extreme compression fibre, the value ηfcd should be reduced by 10%.

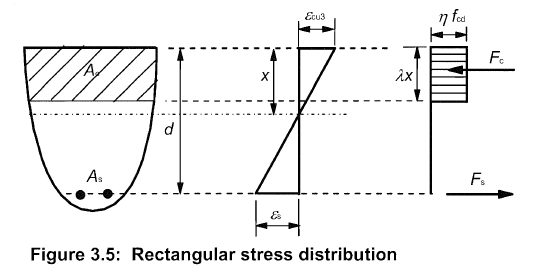Figure 3.5: Rectangular stress distribution

여기서 Note가 등가응력 사각형 적용할 때 주의할 사항이다. 즉 원형 단면(삼각형 단면)과 같이 압축측으로 갈수록 폭이 좁아지는 형상에 등가응력사각형을 사용하려 할 때 적용해야 한다. 

도로교설계기준(한계상태설계법) 해설 2015에는 다음과 같은 내용이 있다.

5.5.1.6 응력-변형률 관계

해설(2) 휨부재의 단면설계에서 사용하는 콘크리트의 응력-변형률 관계는 기본적으로 그림 5.5.2에 보인 포물-사각형 곡선(parabola-rectangle diagram;p-r곡선)으로 나타내고 있다. 이 곡선은 부재 단면의 중립축 위치를 산정하는데 적용할 뿐만 아니라, 압축 연단의 한계변형률 결정에도 적용한다. 그러나 콘크리트의 탄성계수 Ec를 이 곡선의 접선으로 산출하여 사용할 수는 없다. 휨부재에서 압축 연단의 콘크리트 변형률이 극한변형률 εcu에 도달할 때를 극한한계상태라고 한다. 이 극한한계상태일 때 단면 압축합력의 크기와 작용점은 실제 설계에 긴요하게 사용된다. 따라서 압축합력의 크기를 나타내는 계수 α, 작용점 위치를 나타내는 계수 β는 콘크리트 강도 등급에 따라 해설 표 5.5.3의 값을 적용할 수 있다. 이 표에 정리된 α와 β의 값들은 부재 단면이 사각형일 때(압축 영역이 사각형인 경우) 적용하는 값이며, 원형 또는 삼각형 단면 등과 같은 사각형이 아닌 단면에서는 적용되지 않는다. 부재 단면의 압축 영역이 사각형이 아닌 경우는 포물-사각형 곡선의 응력 분포를 적용하거나, 이와 등등한 결과를 제공하는 등가직사각형 응력 블록을 적용할 수 있다. 등가직사각형 응력블록을 적용할 때에는 Ф_c(α_co fck)에 응력 블록의 응력 크기를 나타내는 계수 η를 곱하여 응력의 크기를 구하고, 등가직사각형 응력의 깊이는 중립축 깊이에 계수 β1을 곱하여 구한다. 등가직사각형 응력블록의 계수 η와 β1의 값들은 콘크리트 강도 등급에 따라 해설 표5.5.3의 값을 적용할 수 있다.

해설 그림 5.5.1 단면설계를 위한 응력-변형률 곡선의 극한한계변형률 εcu 분포(이재훈 등, 2011)

도로교설계기준(한계상태설계법) 해설 2015 해설 표5.5.3

해설에서 말하는 포물-사각형 곡선의 응력분포와 등등한 결과를 제공하는 등가직사각형 응력불록은 어떻게 계산하는 것일까?

콘크리트구조한계상태설계(김우 저)  p239에서는 다음과 같이 설명하고 있다.

콘크리트구조한계상태설계(김우 저) 그림 5.6

특히, 40MPa 이하의 보통강도 콘크리트에서는 γ=1이 되어서 등가 사각형 응력 블록을 편하게 사용할 수 있게 된다. 즉 등가 사각형 응력 블록의 깊이 a=0.8c이고 그 합력의 작용점 깊이는 0.4c가 된다. 이 값은 부재 단면이 직사각형일 때(압축 영역이 사각형인 경우) 작용하는 값이며, 원형 또는 삼각형 단면 등과 같은 직사각형이 아닌 단면에는 적용되지 않는다. 만일 콘크리트 압축 영역의 형상이 중립축으로부터 멀어지면서 폭이 작아지는 경우에는 γ=0.95를 적용하여 간단히 계산할 수 있다.