하늘땅

Biaxial bending interaction diagrams for reinforced concrete column design solution The steps to calculate biaxial flexural strength of a rectangular reinforced concrete column for a given nominal axial strength and moment ratio of biaxial bending moments are as follows: 1. assuming a value for the angle of the neutral axis (a) and the neutral axis depth (c) to calculate the strain values in each reinforcement layer 2. Calculate the forces values in the concrete (Cc) and reinforcement layers (Fst) 3. Calculate Pn, Mnx/Mny using the following equations the procedure above should be repeated until the calculated Pn, and Mnx / Mny are euqal to the given Pn, and Mnx/Mny. The following figure demonstrates the procedure explained above: 출처: Biaxial Bending Interaction Diagrams for Rectangular Reinforced Concrete Column Design (ACI 318-19) Structure Point https://skyground21.tistory.com/entry/Biaxial-bending-interaction-diagram

line wrap 수식 줄넘김   Ctrl + enter

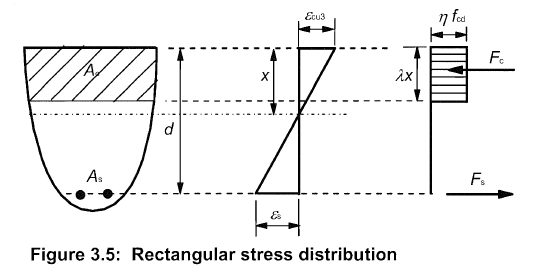
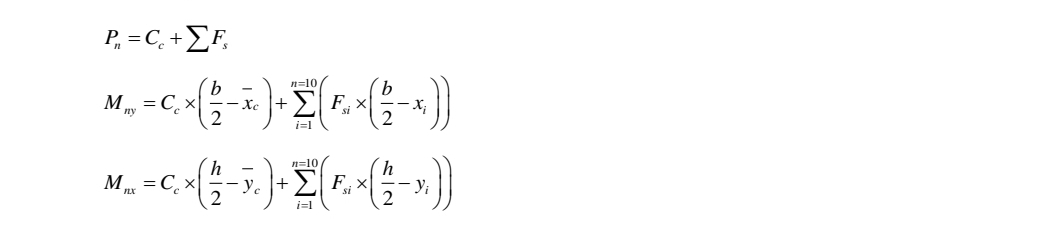 등가응력 사각형의 적용 EN 1992-1-1:2004 3.1.7 Stress-strain relations for the design of cross-sections (3) A rectangular stress distribution (as given in Figure 3.5) may be assumed. The factor λ, defining the effective height of the compression zone and the factor η, defining the effectivestrength, follow from: λ = 0,8 for fck ≤ 50 MPa  (3.19) λ = 0,8 - (fck -50)/400 for 50 < fck ≤ 90 MPa (3.20) and η = 1,0 for fck ≤ 50 MPa  (3.21) η = 1,0 - (fck -50)/200 for 50 < fck ≤ 90 MPa (3.22) Note: If the width of the compression zone decreases in the direction of the extreme compression fibre, the value ηfcd should be reduced by 10%. Figure 3.5: Rectangular stress distribution 여기서 Note가 등가응력 사각형 적용할 때 주의할 사항이다. 즉 원형 단면(삼각형 단면)과 같이 압축측으로 갈수록 폭이 좁아지는 형상에 등가응력사각형을 사용하려 할 때 적용해야 한다.  도로교설계기준(한계상태설계법) 해설 2015에는 다음과 같은 내용이 있다. 5.5.1.6 응력-변형률 관계 해설(2) 휨부재의 단면설계에서 사용하는 콘크리트의 응력-변형률 관계는 기본적으로 그림 5.5.2에 보인 포물-사각형 곡선(parabola-rectangle diagram;p-r곡선)으로 나타내고 있다. 이 곡선은 부재 단면의 중립축 위치를 산정하는데 적용할 뿐만 아니라, 압축 연단의

 wxMaxima can be made to execute commands at every start-up by placing them in a text file with the name wxmaxima.rc in the user directory. This directory can be found by typing maxima_userdir; 사용자 디렉터리에 wxmaxima.rc라는 이름의 텍스트 파일에 명령을 저장하여 시작할 때마다 명령을 실행하도록 wxMaxima를 설정할 수 있습니다. 이 디렉토리는 maxima_userdir을 입력하면 찾을 수 있습니다;

 How To CREATE and MODIFY SHAPES Rectangle (R) Line (L) Arrow (Shift + L) Ellips (O) Polygon Star Place image/video... (Ctrl + Shift + K) Pen tool Shape customization  manipulating vertices  corner rounding  Boolean operations 점을 선택하고 Ctrl + J 하면 점과 점 사이가 연결된다.

  How to Crop Images into Shapes in Figma 1. make shape 2. sent to back the shape behind image ( [ ) 3. select both shape and image 4. Use as mask (Ctrl + Alt + M)

나라별 철근 규격 비교 KDS 3504 ASTM STANDARD JIS G3112 CSA G30.18 D10에서 D29까지는 대한민국, 미국, 일본이 동일하다고 볼 수 있다. 참고로 #3철근은 3/8inch이다. d

 image crop in figma 1.이미지 선택 2.오른쪽 사이드바에서 이미지 썸네일 선택 3. 옵션을 Crop으로 변경 4. 이미지 crop가능함. 단축키 : Alt+doubleclick

 LiDAR(라이다)란 Light Detection And Ranging (빛을 통한 검출과 거리 측정)의 약칭으로, 근적외광 및 가시광, 자외선을 사용하여 대상물에 빛을 비추고, 그 반사광을 광 센서를 통해 검출하여 거리를 측정하는 리모트 센싱 (떨어진 위치에서 센서를 사용하여 검출) 방식을 말한다. Laser Imaging Detection And Ranging (레이저 화상 검출과 거리 측정)이라고도 하며, 대부분은 근적외 레이저 광을 펄스 상태로 조사 (照射)하고, 대상물에 닿아 반사될 때까지의 시간 차를 계측한다. LiDAR는 대상물까지의 거리뿐만 아니라, 위치 및 형상까지 정확하게 검출할 수 있다.

Since wxMaxima 0.8.2 you can also insert images into your documents.  Use 'Cell->Insert Image...' menu command. image copy and paste also can do insert image

  the '[]' operator tried to extract an element of a list, a matrix, an equation or an array.  But instead of an integer number something was used whose numerical value is unknown or not an integer.  Floating-point numbers are bound to contain small rounding errors and therefore in most cases don't work as an array index thatneeds to be an exact integer number. '[]' 연산자가 목록, 행렬, 방정식 또는 배열의 요소를 추출하려고 시도했습니다.  그러나 정수 대신 숫자를 알 수 없거나 정수가 아닌 다른 숫자가 사용되었습니다.  부동 소수점 숫자는 작은 반올림 오차를 포함할 수밖에 없으므로 대부분의 경우 정확한 정수여야 하는 배열 인덱스로는 작동하지 않습니다.