Matrix menu

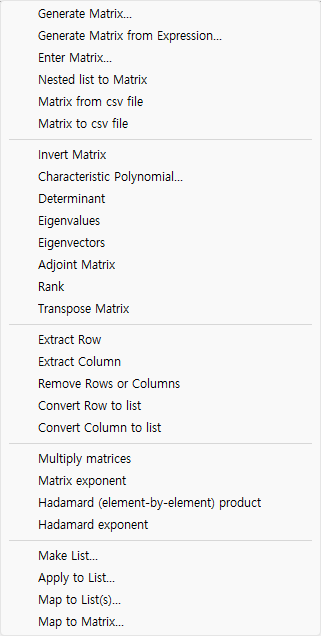 Matrix menu

Matrix menu
Matrix menu


Generate Matrix... 
Generate Matrix from Expression... 
Enter Matrix.. 
Nested list to Matrix 
Matrix from csv file 
Matrix to csv file 

Invert Matrix: 
Characteristic Polynomial... 
Determinant 
Eigenvalues 
Eigenvectors 
Adjoint Matrix 
Rank 
Transpose Matrix 

Extract Row 
Extract Column 
Remove Rows or Columns 
Convert Row to list 
Convert Column to list 

Multiply matrices 
Matrix exponent 
Hadamard (element-by-element) product 
Hadamard exponent 

Make List. 
Apply to List.. 
Map to List(s).. 
Map to Matrix...

댓글

댓글 쓰기

이 블로그의 인기 게시물

Temperature effects_maturity

  In the   CEB-FIP Model Code 90 ,   maturity   is a concept used to predict the rate at which concrete gains strength based on temperature and time.   Eq. (2.1-87)   is used to calculate the   maturity-adjusted time   t_T$ $​ , which accounts for the effects of temperature on concrete's strength development. \(  S=\int d^{4} x\left(\frac{R}{2 \kappa}\right) \) begin{eqation} S=\int d^{4} x\left(\frac{R}{2 \kappa}\right) end{equation} Definition of Equation (2.1-87): The maturity-adjusted time tTt_T tT​  is calculated as: tT=∫t0texp⁡[QR(1T0−1T(τ))]dτt_T = \int_{t_0}^{t} \exp \left[ \frac{Q}{R} \left( \frac{1}{T_0} - \frac{1}{T(\tau)} \right) \right] d\tau tT​=∫t0​t​exp[RQ​(T0​1​−T(τ)1​)]dτ$$ Where: tTt_T tT​  = maturity-adjusted time (in days) tt t  = real elapsed time (in days) t0t_0 t0​  = start time for the calculation (usually 0) QQ Q  = activation energy for hydration process, typically around 33,500 J/mo...
자세한 내용 보기